Machen wir uns zunächst mit einigen Grundlagen der kryptografischen Verfahren vertraut. Zentral ist hier der Unterschied zwischen symmetrischer und asymmetrischer Kryptografie.
Symmetrische vs. asymmetrische Kryptografie
Bei der symmetrischen Kryptografie gibt es meist nur einen Schlüssel. Mit diesem wird sowohl verschlüsselt als auch entschlüsselt. Bei einigen symmetrischen Verfahren können die Schlüssel zwar auch verschieden sein, sind aber einfach voneinander berechenbar, und das in beide Richtungen.
Bitcoin basiert hingegen auf asymmetrischer Kryptografie. Hier existieren zwei verschiedene Schlüssel: einer, um etwas zu verschlüsseln und ein zweiter, um etwas zu entschlüsseln. Dieses Verfahren wird auch oft als Public-Key-Verfahren bezeichnet. Der Name weist darauf hin, dass Person A mit Hilfe eines öffentlichen Schlüssels etwas für Person B verschlüsseln kann. Zum Entschlüsseln ist dann nur Person B mit ihrem privaten Schlüssel in der Lage. Den privaten Schlüssel darf man also niemals öffentlich machen, den öffentlichen Schlüssel schon. Damit das Verschlüsseln mit dem einen Schlüssel und das Entschlüsseln mit dem anderen funktioniert, gibt es zwischen den beiden Schlüsseln eine mathematische Beziehung. Bei Bitcoin wird hier die Elliptische-Kurven-Kryptografie angewendet. Eine solche Beziehung wird auch als Einwegfunktion oder “Trapdoor Function” bezeichnet.
Es ist leicht und effizient, von einem Wert A einen Wert B zu berechnen. Aber mit heute zur Verfügung stehender Rechenleistung ist es unmöglich, in einem angemessenen Zeitrahmen von Wert B auf Wert A zu schließen. Das wird auch als Problem des diskreten Logarithmus bezeichnet, und man hofft in der Kryptografie, dass es für dieses Problem nie eine Lösung geben wird.
Problem des diskreten Logarithmus
Um das Problem des diskreten Logarithmus zu verstehen, betrachten wir die folgende Gleichung: gx mod p = S. Dabei soll eine Lösung für x gefunden werden. p ist eine Primzahl (zum Beispiel 11) und g ein Generator (zum Beispiel 2). Die Variablen g, p und S sind alles natürliche Zahlen. In der Kryptografie wäre S der öffentliche Schlüssel und x der private Schlüssel. Versucht man in dieser Gleichung x zu berechnen, wenn S gegeben ist (zum Beispiel 10), dann kann man das nur mit Probieren erreichen. Unsere Gleichung mit eingesetzten Zahlen sieht nun so aus: 2x mod 11 = 10. Abbildung 1 zeigt eine Reihe von Versuchen, Werte für x herauszufinden, die ein S von 10 ergeben.
Wenn man für x also 5 einsetzt, kommt man auf 10. Folglich wäre der private Schlüssel 5. Bei x = 10 sieht man, dass S wieder 1 ist, was wir bei x = 0 auch hatten. Die Werte von S sind zyklisch und beginnen wieder von vorne. Es gibt also mehrere Werte für x, die einen Wert von 10 für S ergeben.
Durch Ausprobieren haben wir nun eine Lösung gefunden. Das mag mit kleinen Zahlen funktionieren, mit sehr großen Zahlen ist das aber unmöglich oder würde sehr lange dauern. Anwendungsbeispiele, die auf dem diskreten Logarithmus basieren, sind Diffie-Hellman-Schlüsselaustausch, Elgamal-Signaturverfahren, DSA-Verfahren oder das Elliptische-Kurven-Kryptosystem, das bei Bitcoin verwendet wird.

Public-Key-Verfahren bei Bitcoin
Bitcoin verwendet die elliptische Kurve, um den öffentlichen Schlüssel aus dem privaten Schlüssel zu erzeugen. Eine andere Möglichkeit wäre RSA gewesen. Ein privater Schlüssel aus 256 Bits bei einer elliptischen Kurve ist jedoch so sicher wie ein 3 072 Bit langer RSA-Schlüssel. Kleinere Schlüssel sind einfacher zu verwenden und zu handhaben.
Die elliptische Kurve, die bei Bitcoin verwendet wird, heißt secp256k1. Um den öffentlichen Schlüssel aus einem privaten Schlüssel zu berechnen, wird auf der elliptischen Kurve eine geometrische Punktaddition beliebig oft durchgeführt, ausgehend von einem vorgegebenen Basispunkt. Bei Bitcoin entspricht das “beliebig oft” dem privaten Schlüssel, der durch einen Zufallsgenerator erzeugt wurde. Das Resultat ist der öffentliche Schlüssel.
Was ist bei Bitcoin verschlüsselt?
Wenn bei Bitcoin also von “Verschlüsselung” die Rede ist, handelt es sich um die beschriebene asymmetrische Kryptografie. Aber was wird denn nun verschlüsselt? Sind es die Transaktionen, bei denen die Bitcoins einen anderen Besitzer erhalten? Wenn man die Blöcke von Bitcoin allerdings genauer betrachtet, beispielsweise mit einem Bitcoin-Explorer, kann man einen Block sehen, diesen öffnen und dann eine Transaktion anwählen. Die Transaktion besteht aus Inputs und Outputs. Man erkennt genau, von welchen Adressen zu welchen Adressen der Werteaustausch stattgefunden hat und mit welcher Betragshöhe. Es lässt sich also alles anzeigen und lesen, weil es eben nicht verschlüsselt ist.
Signierung dank asymmetrischer Kryptografie
Mit einem Schlüsselpaar der asymmetrischen Kryptografie kann aber nicht nur verschlüsselt, sondern auch signiert werden. Bei Bitcoin werden Transaktionen signiert und nicht verschlüsselt. Mit anderen Worten kann bei Bitcoin damit sichergestellt werden, von wem eine Transaktion erstellt und ob diese unterwegs nicht verfälscht wurde. Es wird eine unverschlüsselte Transaktion T erstellt und danach von Person A signiert (Abb. 1).
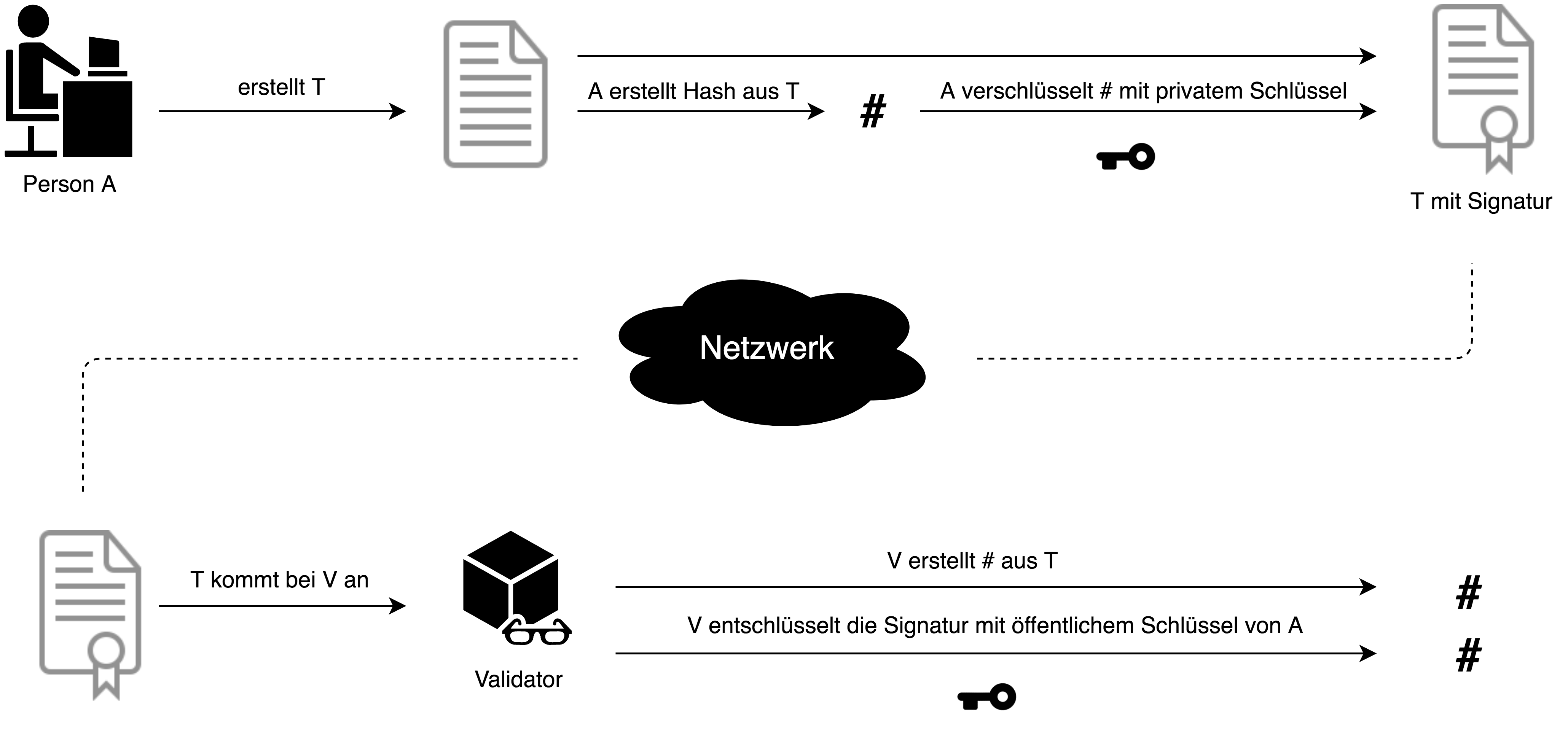
Die in der Abbildung gezeigte Signatur ist vereinfacht und entspricht nicht der vollständigen Signatur von Bitcoin. Bei Bitcoin muss die Signatur zusätzlich erweitert werden und beweisen können, dass der Wert, den man in der Transaktion übertragen möchte, tatsächlich der Person gehört, die die Transaktion erstellt hat, ohne den privaten Schlüssel offenzulegen. Hier soll “signieren” vereinfacht heißen, einen Hash der Transaktion T zu erstellen und danach diesen Hash mit dem privaten Schlüssel zu verschlüsseln, hier abgekürzt EHT (Encrypted Hashed Transaction). In der Transaktion T befindet sich auch der öffentliche Schlüssel von Person A. T und EHT (Signatur) werden nun an das Netzwerk gesendet. Beim Zielort von T kann validiert werden, ob T unterwegs nicht abgeändert wurde. Beispielsweise darf der Transaktionsbetrag nicht geändert werden. Dazu wird der öffentliche Schlüssel von Person A aus T genommen und damit EHT entschlüsselt, es bleibt der Hash von T. Der Empfänger kann jetzt aus T einen eigenen Hash-Wert erstellen, denn der Hash-Algorithmus ist bekannt. Dann kann er überprüfen, ob diese beiden Hash-Werte identisch sind. Sind sie nicht identisch, wurde T irgendwo auf dem Weg abgeändert und wird somit verworfen. Es ist auch bewiesen, dass die Signatur von A stammen muss,ansonsten könnte die Signatur EHT nicht mit dem öffentlichen Schlüssel von A entschlüsselt werden. Das heißt also: Ändert ein Angreifer T ab, muss er auch eine neue Signatur erstellen und,weil er den privaten Schlüssel von A nicht kennt, einen eigenen verwenden. Verwendet er einen eigenen privaten Schlüssel, muss er auch seinen passenden öffentlichen Schlüssel in T als Absender hinterlegen, und somit ist T nicht mehr von A.
Transaktion in Bitcoin
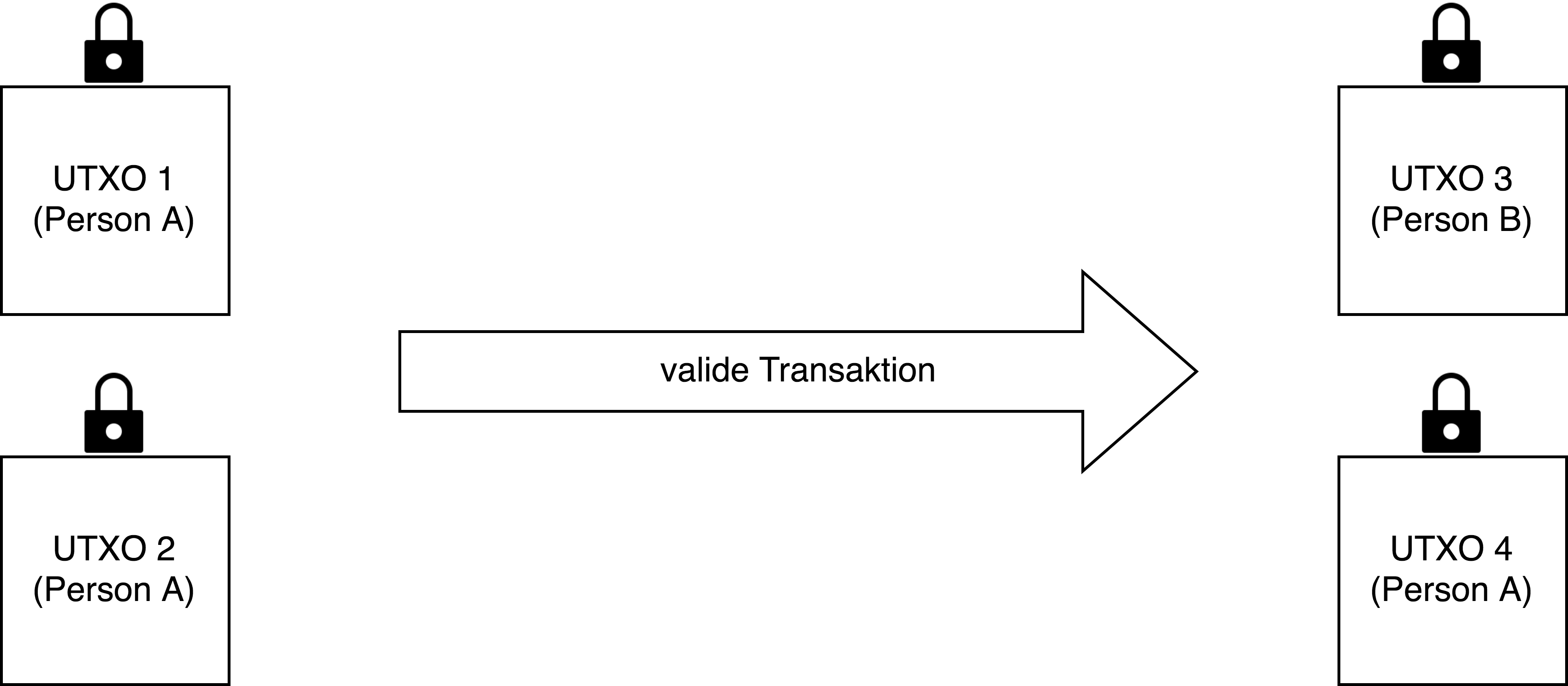
Eine Transaktion in Bitcoin besteht aus Input(s) und Output(s) und verschiebt Werte von einer Person zu einer anderen oder genauer gesagt, zu der Person, die den privaten Schlüssel kennt. Inputs sind immer Outputs von vorhergehenden Transaktionen, die noch nicht verbraucht wurden und deshalb “unspent Transaction Outputs” (UTXOs), genannt werden. Damit jemand einen UTXO nutzen kann, muss er in der Lage sein, diesen zu entsperren. Wird eine Transaktion im Bitcoin-Netzwerk akzeptiert und kommt in einen Block, dann sind die UTXOs danach verbraucht und können nicht mehr für neue Transaktionen verwendet werden. Durch die Transaktion entstehen aber wieder neue UTXOs. Diese sind dann für neue Personen gesperrt oder möglicherweise auch für dieselbe Person, wenn es sich beispielsweise um Wechselgeld handelt. Abbildung 3 veranschaulicht diesen Zusammenhang. In Klammern steht jeweils die Person, die den UTXO entsperren kann, wenn sie eine valide Transaktion mit nötiger Signatur erstellt. Die Transaktion wurde in diesem Beispiel von Person A erstellt. Empfänger des Werts ist Person B, Person A erhält das Wechselgeld. Die Summe aller Inputs muss immer gleich der Summe der Outputs sein, abzüglich der Transaktionsgebühren, die man dem Miner überlassen möchte, damit die eigene Transaktion möglichst schnell den Weg in einen Block findet. Je spendabler die Transaktionsgebühr ist, desto eher ist ein Miner bereit, die Transaktion schnell in einen Block aufzunehmen. Nachdem die Transaktion hier im Beispiel den Weg in einen Block gefunden hat, sind UTXO 1 und UTXO 2 verbraucht, UTXO 3 und UTXO 4 sind neu entstanden.
Output einer Transaktion
Ein Output einer Transaktion in Bitcoin ist für eine spezifische Person bestimmt. Diese Person ist in der Transaktion mit dem öffentlichen Schlüssel vermerkt. Nur die Person, die eine gültige Signatur für den UTXO erstellen und somit das Schloss öffnen kann, kann diesen Output wieder als Input bei einer neuen Transaktion verwenden. Dieses Schloss wird in Bitcoin als Locking Script bezeichnet, das mit einem Unlocking Script in einer nachfolgenden Transaktion geöffnet werden kann. Der Miner prüft dabei in einer Art Stackverarbeitung, ob das Locking Script mit dem Unlocking Script zusammenpasst. Ist das der Fall und alles andere in der Transaktion ist auch valide, entsteht wieder ein neuer Output, der wiederum für eine neue Person – oder genauer für deren öffentlichen Schlüssel – gesperrt ist. Diese oben erwähnte Signatur kann nur mit dem korrespondierenden privaten Schlüssel generiert werden, von dem auch der öffentliche Schlüssel erstellt wurde, der als Empfänger in einer früheren Transaktion vermerkt ist. Man muss also nicht seinen privaten Schlüssel zeigen, um zu beweisen, dass man dieses Schloss öffnen kann. Es reicht sozusagen ein Einwegpasswort, das aus dem privaten Schlüssel erzeugt wurde und nur für diese eine Transaktion gültig ist. Es wäre ja verheerend, wenn in der nicht verschlüsselten Transaktion der private Schlüssel stehen müsste. Mit diesem Schlüssel könnte ein Dieb alle anderen UTXOs verbrauchen, die nicht in dieser Transaktion enthalten waren.
Signatur bei Bitcoin
Aus dem privaten Schlüssel wird also eine Signatur erstellt. Diese Signatur kann beweisen, dass der Ersteller der Signatur auch den privaten Schlüssel kennen muss, der zum öffentlichen Schlüssel passt, mit dem der UTXO gesperrt wurde. Anstatt den privaten Schlüssel preiszugeben, reicht die Signatur, um den UTXO zu entsperren. Das ist mit Mathematik auf der elliptischen Kurve möglich. Das bei Bitcoin verwendete Verfahren, um die Signatur zu erzeugen, heißt “Elliptic Curve Digital Signature Algorithm” (ECDSA). Als Analogie könnte eine Person beweisen, dass sie den Zahlencode eines Schließfachs kennt, indem sie das Schließfach nach der Schließung wieder öffnen kann, ohne den Zahlencode preisgeben zu müssen. Dieser Beweis muss für alle Inputs einer Transaktion erbracht werden, damit eine Transaktion als gültig angesehen werden kann. Ist die Signatur für die zu entsperrenden UTXOs falsch, ist die Transaktion ungültig und wird verworfen. Da diese Signatur für die ganze Transaktion erstellt wurde, ist sie auch nur für diese Transaktion gültig und kann später nicht für weitere verwendet werden. Die Signatur ist also eine Art Einwegpasswort für diese eine Transaktion.
Locking Script und Unlocking Script
Ein Miner überprüft bei einer eingehenden Transaktion T2 (Abb. 4), ob das Unlocking Script auf das Locking Script der UTXOs passt. Dabei wird ein Teil der nötigen Informationen aus der früheren Transaktion T1 genommen, in der sich die UTXOs befinden. Der andere Teil stammt aus der aktuellen Transaktion T2, die es zu validieren gilt. UTXOs aus früheren Transaktionen können dabei auf verschiedene Art und Weise gesperrt sein, je nachdem, was die vorhergehenden Transaktionen beabsichtigten. Das sind “Pay to Pubkey” (P2PK), “Pay to Pubkey Hash” (P2PKH), “Pay to Multisig” (P2MS) oder “Pay to Script Hash” (P2SH). Um den Rahmen dieses Artikels nicht zu sprengen, wollen wir nur das einfachste Locking Script P2PK veranschaulichen. Am meisten wird heute P2PKH verwendet, da es eine zusätzliche Sicherheitsebene einfügt. In diesem Fall können UTXOs nicht einmal gestohlen werden, wenn von einem öffentlichen Schlüssel der private Schlüssel berechnet werden könnte und somit die Elliptische-Kurven-Kryptografie gebrochen würde.
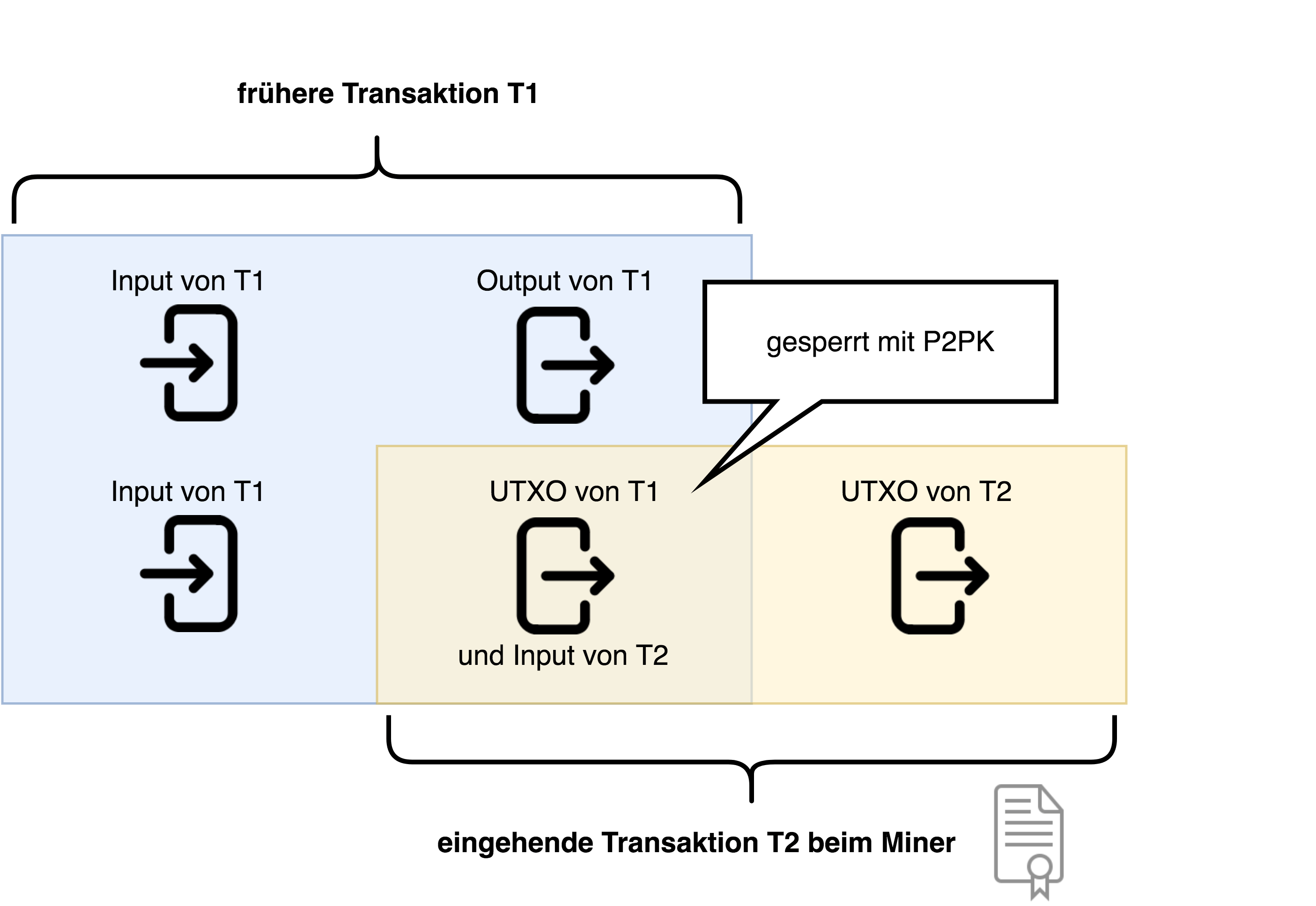
Die Outputs von T1 sind also mit P2PK gesperrt, das bedeutet: gesperrt für einen bestimmten öffentlichen Schlüssel. Diese UTXOs können nur mit einer Signatur geöffnet werden, die vom privaten Schlüssel erzeugt wurde, aus dem auch der öffentliche Schlüssel hervorging. Ein Miner kann das mit einer Art Stackverarbeitung überprüfen. Als Parameterdaten werden dabei der öffentliche Schlüssel aus T1, für den die UTXO gesperrt wurde, und die Signatur von T2 benötigt. Zu beachten ist, dass der private Schlüssel, aus dem der öffentliche Schlüssel erzeugt wurde, hier nicht notwendig ist. Dank der Elliptischen-Kurven-Kryptografie ist das möglich. Die zwei gegebenen Parameter aus den beiden Transkationen müssen nun interagieren können, damit ein Miner beurteilen kann, ob die eingehende Transaktion valide ist oder nicht. Dafür stellt die Script-Sprache von Bitcoin sogenannte Operatoren zur Verfügung. Einer davon ist CHECKSIG, mit dem die Signatur überprüft wird. CHECKSIG ist Teil des Locking Scripts und deshalb auch Teil von T1.
Das gesamte Script mit Daten und Operator sieht, nachdem der Miner es zusammengefügt hat, nun so aus: öffentlicher Schlüssel des Empfängers von T1, CHECKSIG-Operator als Bestandteil des Locking Scripts von T1 und Signatur von T2. Lässt der Miner dieses Script in der Stackverarbeitung laufen, kann er danach beurteilen, ob die Transaktion gültig ist oder nicht. Ist sie nicht gültig, wird sie vom Miner nicht in den Block aufgenommen.
