Source note: Dieser Artikel ist ursprünglich in Ausgabe 05/2018 der Zeitschrift Java aktuell erschienen. Die Veröffentlichung auf innoq.com erfolgt mit freundlicher Genehmigung von https://www.ijug.eu/. Publisher: iJUG e.V Publication: Java aktuell Edition: 05/2018
In diesem Artikel geht es um die Möglichkeit, bei Legacy-Anwendungen Regressionstests anhand des Quellcodes zu generieren, um vor einem möglichen Refactoring Tests erzeugt zu haben. Diese sollen sicherstellen, dass die Anwendung nach dem Refactoring noch genauso funktioniert wie vorher. Hier gibt es einige interessante Ansätze und auch einige Tools, die diese implementieren. Der Artikel zeigt zwei mögliche Ansätze.
Im Projektalltag hat man es häufig mit Legacy-Anwendungen zu tun, die weiterentwickelt und gewartet werden müssen. Meist sind diese Anwendungen „historisch gewachsen“ und das Finden von Bugs oder das Einbauen neuer Features ist schwierig und langwierig. Ein Refactoring ist bei einem System in der Wartungs- und Betriebsphase meistens schwierig unterzubringen, vor allem, wenn der anschließende Testaufwand groß ist. Ein Anfang wären Unit-Tests, welche die technische Funktionalität des Systems sicherstellen. Leider sind gerade häufig in den „historisch gewachsenen“ Anwendungen Unit-Tests eine Seltenheit. Um so praktischer wäre es, wenn man in dieser Situation ohne großen Zeitaufwand automatisch Unit-Tests erzeugen könnte. Diese Tests müssten keine gut lesbaren Unit-Tests sein, wie sie ein Entwickler schreiben würde. Es würde schon reichen, wenn man vor einem Refactoring per Knopfdruck Unit-Tests erzeugen könnte, die man nach erfolgtem Refactoring laufen lassen könnte, um die vorherige Funktionalität sicherzustellen – mit anderen Worten – Generierung von Regressionstests. Das Prinzip nachdem man dabei vorgehen kann ist folgendes: Man hat eine Klasse, die man testen möchte, das System unter Test. Diese ruft man nun im Testfallgenerator auf und merkt sich die Ausgabewerte. Dann erzeugt man mit den gleichen Aufrufparametern und den gemerkten Ausgabewerten einen Testfall. Das Ziel ist es, für alle möglichen Pfade des Systems unter Test einen Testfall zu erzeugen. Die Schwierigkeit hierbei ist, die richtigen Aufrufparameter zu finden.
Der Ansatz „Zufallsdaten“
Der erste Ansatz hierzu wäre ein simpler Codegenerator, der eine Testklasse generiert, in der Methode für Methode des Systems unter Test Testfälle erzeugt werden, in denen die Methoden jeweils einfach mit Zufallsdaten aufgerufen werden, bis die Testcoverage 100% beträgt. Leider ist dieses Prinzip sehr aufwändig, was sehr schnell klar wird, wenn man über eine Methode nachdenkt, die nur einen int-Parameter hat und z.B. eine If-Abfrage, ob dieser Int-Parameter 23 ist:
public class TestValue{
public static boolean is23(int parameter){
if(parameter == 23){
return true;
}
return false;
}
}Im Falle 23 soll etwas anderes getan werden als in allen anderen Fällen. Alleine für eine solche Methode müsste der Zufallsansatz im schlechtesten Fall alle möglichen Integerwerte (232 = 4.294.967.296 Möglichkeiten) durchprobieren. Dieser Ansatz lässt sich durch einfache Maßnahmen verbessern. Eine gute Möglichkeit hierfür ist z.B. den Sourcecode oder Bytecode des Systems unter Test nach Konstanten zu durchsuchen und für diese Konstanten auch Tests zu generieren. Der beschriebene Fall von eben lässt sich so leicht umgehen und auch andere Pfade können so einfach durchlaufen werden. Ein Tool, was tatsächlich JUnit-Tests für eine Klasse generiert und dabei intelligent gewählte Zufallswerte als Basis nimmt, ist Randoop.
Der Ansatz „genetische Algorithmen“
Ein weiterer möglicher Ansatz zum Erzeugen einer möglichst hohen Testcoverage ist die Betrachtung der Thematik als Suchproblem. Nehmen wir als Beispiel hierfür wieder eine If-Abfrage auf einen Int-Parameter, allerdings nicht mehr nur ob dieser den Wert 23 hat, sondern ob er mal 2 genommen den Wert 46 ergibt:
public class TestValueMultiplication{
public static boolean is23(int parameter){
if(parameter * 2 == 46){
return true;
}
return false;
}
}Dieses Problem lässt sich nicht mehr durch clevere Wahl der Integer-Werte aus dem Bytecode lösen, da weder 2 noch 46 als Werte mal 2 genommen 46 ergeben. Als Suchproblem gilt es also einen Parameter zu finden, der die Bedingung „hat multipliziert mit 2 den Wert 23“ erfüllt. Dafür definiert man sich eine Distanzfunktion die einem den Abstand zu dem Wert liefert, in diesem Fall Distanz = |x*2-46|. Ein einfacher Ansatz wäre, auf diese Funktion Hillclimbing (den Bergsteigeralgorithmus) anzuwenden, um nach einem Wert X zu suchen, der die Distanz 0 ergibt, wenn man ihn in die Abstandsfunktion einsetzt:
private static Function<Integer,Integer> distance
= x-> Math.abs(x*2-46);
public static int simpleIntegerHillClimbing(){
int bestValue=Integer.MAX_VALUE;
int currentValue =0;
while(distance.apply(currentValue)!=0){
if(distance.apply(currentValue)<bestValue){
bestValue=distance.apply(currentValue);
}
if(distance.apply(currentValue+1)<bestValue) {currentValue+=1;}
if(distance.apply(currentValue-1)<bestValue) {currentValue-=1;}
}
return currentValue;
}Im Listing handelt es sich um eine sehr einfache Implementierung für das Finden von Integern, die nur funktioniert, wenn es eine Lösung gibt. Für ein Problem wie das Durchlaufen der Abfrage auf den Wert 23 wird man auf diesem Weg relativ schnell eine Lösung finden. Allerdings stößt auch Hillclimbing bei komplizierteren Problemen schnell an seine Grenzen. Ein Beispiel dafür wäre, wenn wir als Bedingung der If-Abfrage nicht mehr nur einen Parameter hätten, sondern 2:
public class TestTwoValues {
private static boolean twoParameters(int x, int y){
if(x==2 && x*y == 46){
return true;
}
return false;
}
}In diesem Fall wäre die Distanzfunktion für unser Suchproblem | x-2 | + | x*y -46 |. Die Angepasste Hillclimbing-Funktion für 2 Parameter sieht schon deutlich komplizierter aus:
private static Function<int[], Integer> distance = (int[] parameters) -> Math.abs(parameters[0] - 2) + Math.abs(parameters[0] * parameters[1] - 46);
public static int[] twoIntegerHillClimbing() {
int lowestDistance = Integer.MAX_VALUE;
int[] current ={0,0};
while (distance.apply(current) != 0) {
if (distance.apply(current) < lowestDistance) {
lowestDistance = distance.apply(current);
}
int[] bestNeighbor=
bestNeighbor(getNeighbors(current));
if (distance.apply(bestNeighbor) < lowestDistance) {
current=bestNeighbor;
}
}
return current;
}
private static int[][] getNeighbors(int[] current) {
int x=current[0], y=current[1];
return new int[][]{{x + 1, y}, {x, y + 1}, {x + 1, y + 1},
{x - 1, y}, {x, y - 1}, {x - 1, y - 1}};
}
private static int[] bestNeighbor(int[][] neighbors) {
return Arrays.stream(neighbors)
.min(Comparator.comparing(neighbor -> distance.apply(neighbor)))
.get();
}Dazu kommt, dass diese Funktion in eine Endlosschleife läuft, da Hillclimbing hier an seine Grenzen stößt. Von [6,6] aus angefangen sehen die Schritte wie folgt aus:
neighbors = [[6, 5], [5, 6], [6, 6], [4, 5], [5, 4], [4, 4]]
bestneighbor = [[6, 6]]
distance = 14
neighbors = [[7, 6], [6, 7], [7, 7], [5, 6], [6, 5], [5, 5]]
bestneighbor = [[6, 7]]
distance = 8
neighbors = [[7, 7], [6, 8], [7, 8], [5, 7], [6, 6], [5, 6]]
bestneighbor = [[6, 8]]
distance = 6
neighbors = [[7, 8], [6, 9], [7, 9], [5, 8], [6, 7], [5, 7]]
bestneighbor = [[6, 7]]
distance = 8
neighbors = [[7, 8], [6, 9], [7, 9], [5, 8], [6, 7], [5, 7]]
bestneighbor = [[6, 7]]
distance = 8 […]Wie man sieht, wird an der Stelle [[6,7]] ein lokales Optimum erreicht, das bei der Schrittweite im Bereich seiner Nachbarn keinen besseren Wert mehr erreichen lässt. Genau an dieser Stelle setzen genetische Algorithmen an. Um den Ansatz zu verstehen, lässt sich Hillclimbing einfach weiterverwenden, jedoch verwendet man für das Problem nicht mehr nur einen Ausgangswert pro Parameter, sondern gleich mehrere, man spricht von einer Generation. Man hat also mehrere Einstiegswerte, von denen ausgehend man versucht eine Lösung zu finden. Ziel der mehreren Einstiegswerte ist es, lokale Optima zu vermeiden, da ja durch das Loslaufen von mehreren Punkten mit hoher Wahrscheinlichkeit von einem der Einstiegspunkte auch das globale Optimum erreicht wird. Um von vornherein eine Endlosschleife zu vermeiden, zählt man das Wiederauftauchen der gleichen Nachbarn nach einem Optimierungsschritt. Wenn mehr als zwei Mal die gleichen Nachbarn hintereinander auftauchen, befindet man entweder an einem lokalen oder aber am globalen Optimum, daher kann man die Bedingung der while-Schleife entsprechend anpassen. Danach macht man die Hillclimbing-Funktion parametrisierbar:
public static int[] hillClimbing(int[] current) {
int lowestDistance = Integer.MAX_VALUE;
int[] bestNeighbor;
int circles = 0;
while (circles <= 2) {
if (distance.apply(current) < lowestDistance) {
lowestDistance = distance.apply(current);
}
if (distance.apply(current) == lowestDistance) {
circles++;
}
bestNeighbor = bestNeighbor(getNeighbors(current));
if (distance.apply(bestNeighbor) < lowestDistance) {
current = bestNeighbor;
}
}
return current;
}Aufrufen kann man das ganze dann beispielsweise wie folgt:
public static void main(String[] args) {
Random random = new Random();
int[] bestResult = IntStream.range(0, 100000)
.boxed()
.map(i -> new int[]{random.nextInt(1000), random.nextInt(1000)})
.map(HillClimbing::hillClimbing)
.min(Comparator.comparing(result -> distance.apply(result)))
.get();
System.out.println("bestResult = " + Arrays.deepToString(new int[][]{bestResult}));
System.out.println("distance = " + distance.apply(bestResult));
}In diesem Aufrufbeispiel wird mit 1000 verschiedenen zufälligen Ausgangswertepaaren nach dem globalen Optimum gesucht, am Ende wird der beste gefundene Wert ausgegeben. Dieses Beispiel ist ein stark vereinfachter genetischer Algorithmus, der auf ein bestehendes Suchproblem hin optimiert. Am Ende kann man auf diesem Weg anhand einer Distanzfunktion Werte finden, die einem dabei helfen in Bedingungen zu laufen um bei der Erzeugung eine möglichst hohe Coverage zu erhalten. Ein Tool, das diesen Ansatz für die Generierung von JUnit-Tests verwendet ist EvoSuite.
Ausprobieren
Nun, da zwei verschiedene Ansätze erläutert wurden, stellen wir beide Ansätze auf die Probe. Da das Ziel sein soll, für Legacy-Code echte Regressionstests zu erzeugen, braucht man als erstes einmal Legacy-Code. Hierfür gibt es eine Benchmark-Anwendung, die eine Klasse enthält, die stark verschachtelt ist und viele verschiedene Dinge in einer einzigen Methode tut, etwas, das den Reflex refactorn zu wollen, direkt auslöst. Die Methode in der Klasse tut drei Dinge, je nachdem, was für ein String ihr in einem Parameter namens „state“ übergeben wurde. Die drei Dinge sind einmal das (ineffiziente) Ausrechnen von Primzahlen, das Aufrufen eines Remote-Services für Wetterdaten und das Speichern von Programmiererinnen und Programmierern in einer Datenbank. Natürlich ließe sich dieser Code gut in drei Teile aufteilen, die jeweils eine der drei Aufgaben übernehmen. Genau für ein solches Refactoring wäre es praktisch, wenn man Regressionstests für den bestehenden Code generieren könnte, um sicherzustellen, dass nach dem Refactoring die Funktionalität erhalten geblieben ist.
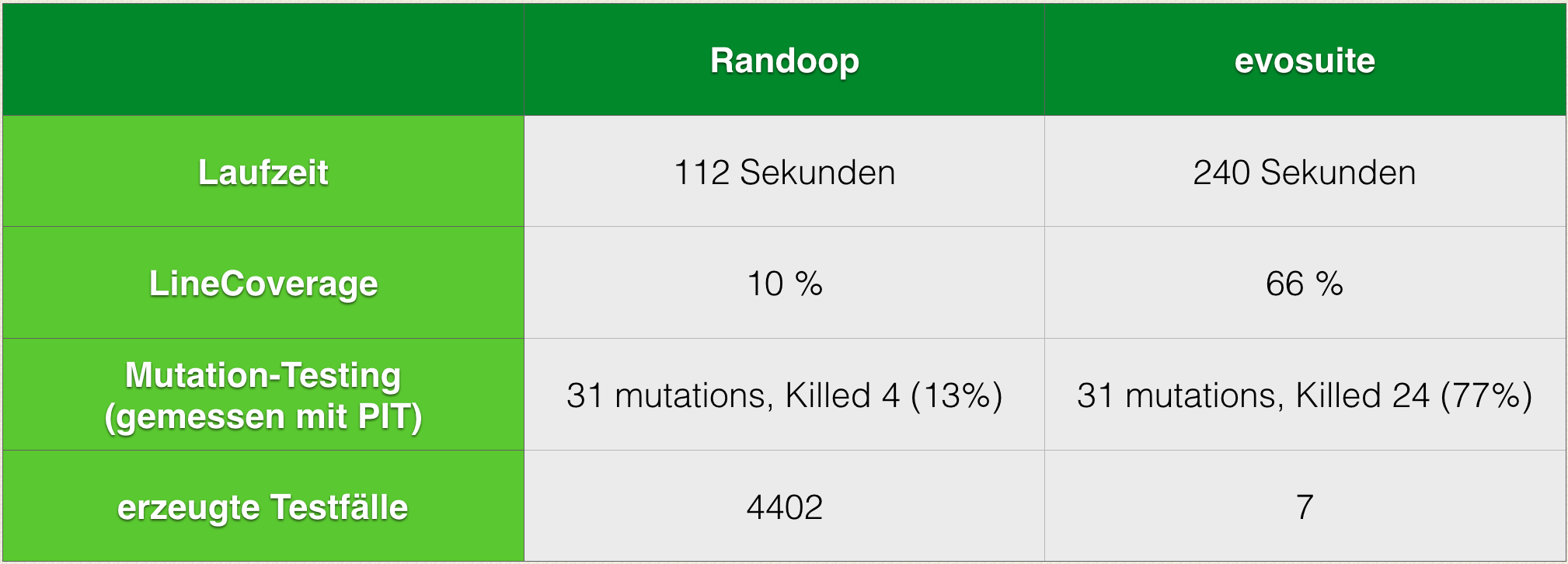
Im nächsten Schritt werden die beiden Tools Randoop und EvoSuite auf diese Methode als Benchmark losgelassen, um genau das zu tun und dann anschließend die Ergebnisse zu vergleichen. Bei Randoop werden für die eine Methode um die 4000 Testfälle erzeugt, die Anzahl variiert etwas. Die erreichte Line-Coverage liegt bei etwa 10%. Dafür braucht Randoop etwa 2 Minuten Laufzeit. EvoSuite erzeugt für die gleiche Methode 7 Testfälle. Diese erreichen eine Line-Coverage von 66%. Die von EvoSuite benannte Dauer für die Generierung dieser Tests liegt bei ca. 4 Minuten. Allerdings sagt die Line-Coverage der erzeugten Testfälle leider noch nichts über deren Qualität aus. Selbst wenn die Testfälle alle Pfade des Codes durchlaufen, ist nicht sichergestellt, dass die Prüfungen in den Testfällen auch eine echte Aussage haben. Trotz 100% Line-Coverage sind ohne sinnvolle Asserts die Testfälle im Grunde wertlos. Um herauszufinden, ob die Assertions in den Testfällen eine sinnvolle Aussage haben kann man Mutation-Testing verwenden.
Beim Mutation-Testing werden vom eingesetzten Tool Mutationen im System unter Test erzeugt und anschließend gemessen, wieviele dieser Mutationen dazu führen, dass Testfälle tatsächlich fehlschlagen. Nur wenn ein Testfall fehlschlägt, gilt die Mutation als eliminiert. Je mehr Mutationen die Testfälle eliminieren, desto aussagekräftiger sind die Assertions in den Tests. Als Tool für Mutation-Testing wurde Pit verwendet, um die anhand des Benchmarks generierten Testfälle zu messen. Hierbei wurden von Pit jeweils 31 Mutationen im Ausgangscode erzeugt. Hiervon konnten die von Randoop generierten Tests 4 Mutationen eliminieren (13%), die Tests von EvoSuite eliminierten 24 Mutationen (77%).